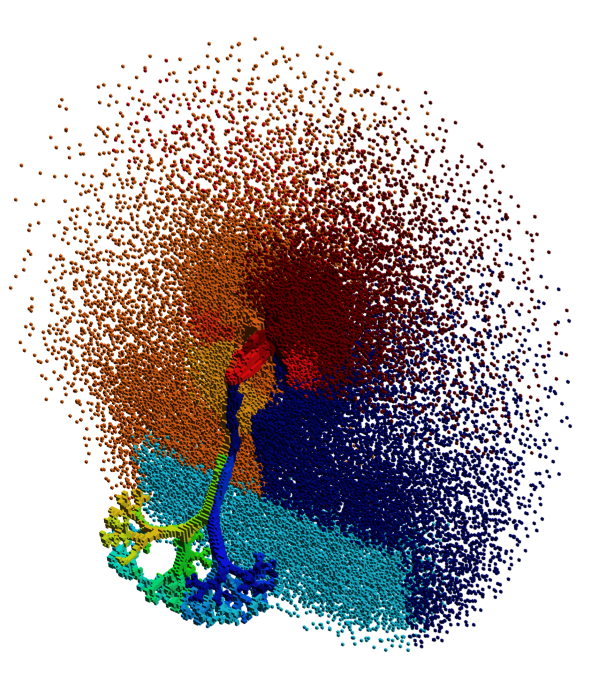
Space filling curve mesh partitioning of the respiratory system
ChEESE partners from the Barcelona Performance Computing Center (BSC) are in charge of Task 3.2, which proposes to explore parallel mesh partitioning strategies to enable dynamic load balance of the different simulation codes.
There are two main families of mesh partitioning methods: topological and geometrical. On one hand, topological partitioning provides well balanced workloads while minimising the interfaces (e.g. METIS, Zoltan, Scotch). However, such methods were originally developed as sequential methods, and their parallel counterparts have a great drawback: the resulting partitioning and its quality depend greatly upon the number of CPUs used. On the other hand, geometrical partitioning methods are based on mesh entity coordinates, which enables an easy parallel treatment and results in a method with good scalability properties. Although limited control on the interface is possible, they provide balanced partitions in a reduced amount of time. This opens the way to dynamic load balancing, to recover from slower computing nodes, or to balance the workload easily across heterogeneous systems.
In Task 3.2 of ChEESE, such methods will be explored, like the Hilbert or Peano Space Filling Curve methods to provide dynamic mesh partitioning to the different codes involved in the Centre of Excellence. The challenge will consist of exploring different strategies for the different numerical methods and programming languages of the simulation codes. At the moment, the library already includes parallel partitioning base on Hilbert Space filling curve. Further work will consist in including Peano Space Filling curve, as well as optimising the performance of the library. Integration with the different codes and systematic testing will also be carried out.
